牟礼神社にある和算の算額：そこにはどのような数学の問題が? 江戸〜明治時代の数学とは? 現代風に解いてみると?

和算の算額とは

「和算（わさん）」というのは江戸時代の日本で独自に発展した数学のことです。「関孝和」という和算家の名前を社会科の授業で習った気がします。では「算額」とは：ウィキペディアの「算額」の冒頭をそのまま引用しますと

算額（さんがく）とは、江戸時代の日本で、額や絵馬に和算の問題や解法を記して、神社や仏閣に奉納したものである。

算額は和算において問題が解けたことを神仏に感謝し、ますます勉学に励むことを祈念して奉納されたと言われる。やがて人の集まる神社仏閣を問題の発表の場として、難問や問題だけを書いて解答を付けずに奉納するものも現れ、それを見て解答や想定される問題を再び算額にして奉納することも行われた。

というものです。要は数学の問題とその解答が額として飾ってある（奉納されている）感じですね。

牟礼神社にも算額があったとは… 知りませんでした

算額というものの存在を聞いたことはありましたが、個人の勝手なイメージとして、日本を代表するかつての著名な一握りの数学家が、どこかの全国的に有名な神社にでも奉納したものだろうと勝手に思っていました。
ところが… 何かをググっていたとき、偶然、長野県の小さな町である飯綱町の牟礼神社にも算額があるとの情報に辿り着きました。これはちょっとした驚きでした。

飯綱町のあたりにも、数学の専門家、ないし愛好家がいらっしゃったという感じでしょうか。いったいどんな職業の方々だったのかとか、興味があります。（これは後日調べてみたいと思います。まだほんのちょっと調べただけですが、かつての和算というのは思いのほか盛んだったようで、算額も色々な場所（神社仏閣等）にあるようですね。）

ちなみに余談ですが、ごく個人的な記憶にある牟礼神社は… 集落の神社として、初詣や祭の場所（七年に一度御柱祭もある）ではあるのですが、日常としては、かつては境内で地元の子供らが野球をして遊んだりしたものでした（今は?）。神社ですから、石畳や、幹が巨大な欅の木等、ボールをイレギュラーバウンドさせる要素が満載の「野球グラウンド」なわけですが、さらに「狛犬に打球を当てたらホームラン」「制札（境内での禁止事項などが書かれた掲示板的なもの）に打球を当てたらホームラン」とかそんなルールもあった気がします。それにしても境内で野球とは罰当たりな?（というかその旨が制札にも書いてあったり?）まあそれは…
ちなみに「飯綱町の河岸段丘」の記事で書きましたが、野球以外にも、冬は参道の坂がソリ遊びの「ゲレンデ」に、あと昔は神社の屋根が茅葺きで（今は銅板葺き?）、屋根を葺き直した後の茅に潜って遊んでいたような… 子供らは神社をただの遊び場としか思っていなかったようです。「神をも恐れぬ」とはこのことか…
おっとっと、余談が過ぎました。

とにかく、このような場所の背後に歴史のある数学の額がひっそりと掲げられていたのですね。何だか不思議なものです。

これは… 調べてみるしかないでしょう

このような経緯で、個人的に和算というものとの意識的な距離が急に縮まりました。その算額がいつ、誰によって作られたのか、そういう興味ももちろんですが、それに加えて、「そこで展開されている数学はどんなものなのか」というのも気になります。

ただ、そういうことをしたい場合、障壁があります。それは例えるなら古典文学を理解するようなもので、古典の文章を直接に読解するには結構な訓練が必要ですよね。現代語訳があればそれを読めばいいでしょうが。同様に数学も古い数学が使われていたらそれを直接理解するのはおそらく困難で、理解するための訓練を積むか、可能ならば現代風に訳されたものを読む、ということが必要になることでしょう。

さて、どうしたものか… 実はこういった算額を研究された先人の方々がいらっしゃり、この牟礼神社の算額に関しても文献があるようなので、まずはそれを参照してみます。

その算額はどんなものか

「和算の館」というサイトがあり、オンラインで日本全国の算額の写真が見られます。すごいですね。何と牟礼神社のものもあり、その画像をここに引用させていただきます。

牟礼神社のものは保存状態が良好で貴重なようです。図の色も割と残っていますね。画像だと文字が少し読みづらいですが、現物だったら普通に問題の文章も読めそうです。
ただ、どうも漢字ばかりで、おそらく和算の問題は漢文で書いてあるのかと。当時の和算とはそういうものだったのでしょうか。達筆な草書でないだけでも読みやすいとは言えますが。
この算額の日付は明治31(1898)10月とあり、ウィキペディアに書いてある江戸でなく明治¹ですね。相対的に新しめ²です。とは言っても2025年現在から127年も前ですけど。ちなみに、最後にある五洲さん（文書中のフルネームは山岸五洲さん）、この算額の清書を担当された方のようですね。

実際にどんな数学の問題なのか、ちょっと気になる

しかし、存在を知ってしまった以上、どのような数学であったのかは気になります。ところが、上に書いたように、全文が漢文で書いてあるようで、数学以前にそもそもそれを読解できるのかという、早くも暗雲が。上の画像だと字そのものが読みづらい問題もあります。
と思っていたら、上記和算のサイトにこれを清書（活字化）・PDF化した文献を発見しました。素晴らしい。算額の画像からなんとなく分かるように、三題あるようで、まずは第一題目を引用させていただきます。これです：

これは… とりあえず少しでも見やすくするように、問題文と図を抜き出してみます。

問題文：

今有如圖輪與菱平之合角相交處設黒點而輪旋菱（輪周一處親菱 自始至終不變之）黒點旋輪周（毎菱之合角輪振回 間者黒點息旋亦從 輪之運行黒 點旋其周）共右旋逐全一周而同時復元處於是黒點運行之軌跡自有成象也菱長（若干）菱平（若干）輪徑（若干）問得成象周及積術如何

（注: ところどころ行が部分的な二行になっていて、注釈ぽくもあるのですがよくわからず。とりあえず丸括弧で囲んでみました。）

これは… まずは旧字体の漢字だらけで面食らいます。ただ、最初に見たときは本気で意味不明でしたが、図と合わせて考えると、円（圖輪）が菱形に沿って右回りに転がって一周する、その時円周上にある点（黒點）が描く軌跡がどうたら、というようなことが書いてある気が… します。

AIの援用?

こりゃーまず問題を言葉として理解するのに相当かかる³な、と思っていたのですが、現代の我々はAI翻訳というチートツール(?)を手に入れつつあります。ではその力を借りましょう。

問題文：

さて、図に示すように、車輪と菱形の角度の交点に黒い点が置かれています。車輪は菱形の周りを回転します（車輪の円周は菱形に近く、最初から最後まで変化しません）。黒い点は車輪の周りを回転します（各菱形の角度で、車輪は前後に振動し、黒い点は回転中に車輪の回転に従って静止します）。それらは一緒に時計回りに回転し、完全な円を描いて元の位置に戻ります。黒い点の軌跡は画像を形成します。菱形の長さ（特定の数値）、菱形の平坦度（特定の数値）、および車輪の直径（特定の数値）。画像の円周と累積方法をどのように決定できますか？

かなりいけてないですか? 元の文章は漢文、すなわち古代の中国語だと思うんですが、それでもかなりいけますね。
というわけでやはり、「円を菱形の周りに転がしたときに円上の点が描く軌跡（の長さ）」の問題のようです。

実はこの漢文を元のテキストから取り出す作業も、OCR（コンピュータ文字認識）の力を借りました。その技術自体は以前からあるものの、昨今はこれもAIを援用することにより、このような古典的な文ですら、かなりの識字率です。

問題の図：

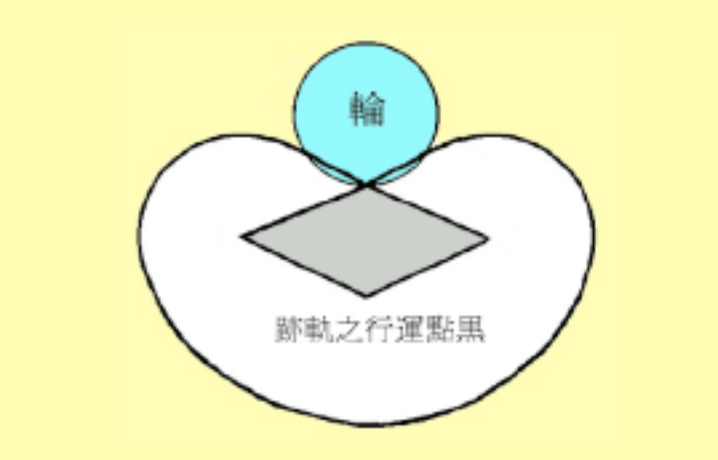
おっとこの独特のラインは… いつか何かの数学系の本で見たような図です。どうやらいわゆる「サイクロイド」（円を平面上で転がした時に円周上の一点が描く軌跡）の応用問題なのか、ということが推測されます。さらに細かく言うとカージオイドの一種かもしれません。一応理解可能な範囲の数学ではありそうな予感??
やはり図は「共通言語」ですね（って、問題文だって日本人が書いたわけですが）。問題文がよくわからなくても図で何となく察しがつくような。

そして解答（「答曰」の部分）：

術日（別求菱面）置菱（以下畧菱之字）長以面二段除之擬弦置一個擬圓徑依術求弧（背積）名（木火）置平以面二段除之擬弦以一個擬圓徑依術求弦（背積）名（土金）置二個平方開之乘木加土乘輪徑二段（名水）置面以圓積率除之（加減）輪徑擬（長短）徑依術求側圓周加水得成象周置長乘平半之（名定）以面幕除之加火金和四段及圓積率乘輪徑加面二段乘輪徑加定得成象積
（若輪與黒點異旋則以面幕除定加火金和四段内減圓積率乘輪徑加面二段乘輪徑加定得異旋之成象積）合問

うーん、これで解答と言われても何のこっちゃですね。ただ断片的に読み取れる情報として

• 加、減、乗、除の字から何か計算式っぽいものを説明しているようではある。
• 「擬弦」という言葉が見受けられ、どうやらこれは今でいう正弦、サイン（\(\sin\)）のこと らしい。ということは和算でも三角関数はあったと。（江戸時代にも、天体観測による暦の計算、伊能忠敬による日本全国の測量等があった以上、三角関数の知識が存在したでしょうね）。あと「側圓」（圓は円の旧字）は楕円のことらしい。が今回は楕円は出てこない気が⁴。サイクロイドのこと? サイクロイドは中国語で「擺線」と書くようです。
• 木、火、水、土、金とか… どうもこれらは変数名? 今ならa, b, c, d, eみたいな感じの?

しかしこのように漢字だらけで、数学の問題および解答だとはにわかには信じ難いですが。そもそも昔の人は数式とかどうやって計算したんでしょう。まさかこういう感じで漢字をだらだら書いたんでしょうか。もしそうなら恐るべしです。

というわけなんですが、こちらもAI翻訳にかけてみます：

菱形の面を別々に求める技法です。菱形（以下、菱形）の長さを面の2つの線分で割り、擬似弦を求めます。擬似円の直径を置き、名（木、火）を用いて円弧（裏積）を求めます。平面を置き、平面を2つの線分で割り、擬似弦を求めます。擬似円の直径を置き、名（土、金）を用いて擬似弦（裏積）を求めます。2つの正方形を置き、木の根を取り、土を加え、車輪の直径（水の2つの線分）を掛けます。面を置き、円積比（加減）で割ります。車輪の直径（長短）を直径とし、技法を用いて側周を求めます。水を加えて像の円周を求めます。長さを置き、平面の半分（「固定」と命名）を掛け、面幕で割ります。火、金属、円積比の4つのセグメントを合計し、車輪の直径と面の2つのセグメントを掛け、車輪の直径と面の直径を掛けて、像積を求めます。
（車輪と黒点の回転が異なる場合は、面のカーテンを一定の数で割り、火、金属、円積比の4つのセグメントを合計し、車輪の直径と面の2つのセグメントを掛け、車輪の直径と一定の数を掛けて、異なる回転の像積を求めます。）複合問題

うむー。それっぽい文章だがところどころおかしい（例えば「金属」とあるのは単に変数を月火水… としたうちの金でしょう）。でも何とかじっくり読めば理解できそう… な気はしてきましたが。それにしても一応AIの翻訳で現代日本語風にはなるわけですね。
あと、どうやら計算の「手順」を書いてあるような感じで、ではなぜその計算手順なのか、という疑問も湧いてきます。

もしかしてこの和算の問題を解くこともAIでできるのかもしれないけど… そうやって出された答えを確認するのが趣旨ではないので、試していません。江戸〜明治の人々がどのような数学を扱っていたかに興味があり、そのためには自分で問題を理解し、その解法を考えてみる必要があります。

では、今の数学を使って実際に解いてみよう

問題を見た以上、理解できるか、解けるかどうかも試してみたいものです。それではいざ!

っておい、まずは漢文の数学問題を解読するところからだろ! AI翻訳しても特に解答の方はまだまだ数学の意味が明快じゃないし。

なのですが、上記の和算のサイトの文献には元の算額の内容が清書してあっただけでなく、問題とその解答が現代風に解説してありました。重ね重ね素晴らしいです。
というわけでここでは問題とその解法を、和算のサイトの文献の解説を参照しつつ、私自身の解釈も含めて（和算の文献の解説では、少なくとも私には初見ではよくわからなかったので）ご紹介したいと思います。
このような数学の問題は、最終的な答えもともかく、むしろそこへ辿り着く過程が重要で、その部分は私自身で考えましたので、以下にご紹介したいと思います。

この問題での重要ポイント

いきなりこの問題の重要ポイント：ただのサイクロイドとどう違うか

ではまず、単純なサイクロイドの問題に帰着できるか検討してみます。サイクロイドならば、色々な数学的性質が知られているので、それを適用することができるはずです。
この問題で円は菱形に接してその周りを回ります。菱形の一辺の長さを \(l\) とすると菱形の周長は \(4l\) です。
では、菱形の一部を切って辺を全部まっすぐに伸ばす感じで、単に全長 \(4l\) の線分上を円が移動すると考えては駄目でしょうか?

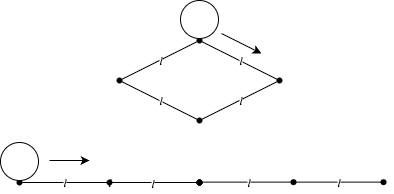
答えは… 駄目です
でも悪くはない着目点で、逆にどこが具体的に駄目なのかを考えることが正解につながります。

ただの直線上を転がるのとの差は：円が菱形の一つの角の直前に到達した時、次の辺に移るためにぐるっと角を回り込まねばならず、まっすぐな直線の上を転がるのに比べて、この「角でぐるっと回る」分、円周上の点が余計に距離を移動します。
ぐるっと回り込む部分以外は直線上と同じになります（角を回り込むときに円の自転は止まっているので、いわば円の回転の位相がずれずに、角の前後で、菱形の辺の上での転がり運動はうまく接続されます）。

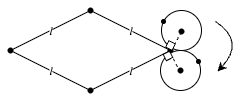
菱形の辺の上を転がっている間は普通のサイクロイドの軌跡ですが、角の部分に着いたら円がぐるっと回ります。この「ぐるっと回る」間は円の一点が菱形の角に固定されているので、平面上を転がるのとは違う運動になり、点の軌跡はサイクロイドでなく「扇形の弧」になります。
その後は次の辺の上を移動し、その間はまたサイクロイドの軌跡になります。そして角で回る… これを繰り返します。

したがって、最終的な答え（点の移動距離）は

「円が菱形の辺の上を転がっている間の点の移動距離」＋「円が菱形の角をぐるっと回る部分での点の移動距離」

となります。これで方針がたちました。良いことです。

具体的な計算

それでは、上の話で出てきた

1. 円が菱形の辺の上を転がっている間の点の移動距離
2. 円が菱形の角をぐるっと回る部分での点の移動距離

をそれぞれ具体的に評価・計算してみます。

その１：円が菱形の辺の上を転がっている間の点の移動距離
以下の図で太い線の矢印で書いた部分の軌跡のことです。

元の問題によると、円が菱形の周りを一周するときに円自体もちょうど一回転（円の自転が一回転というか）するという条件があるようです^{5 6} 。とりあえず元の図（円が転がって描く図形）ではそう見えますね。
そうすると、この軌跡は以下のようなサイクロイドと等価です（菱形の角の位置で、円の半径と辺が90度をなすことに注意してください）。

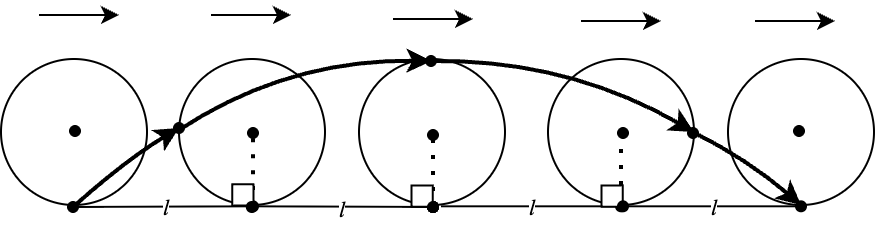
サイクロイドの公式により、サイクロイドのもとになる円が一回転する間に円上の点が移動する距離（＝サイクロイドの軌跡の長さ）はその円の半径の8倍です（既に引用したWikipediaのページ等を参照）。もしこの公式を知らない場合：今の数学ならサイクロイド曲線をパラメーター表示して積分しても出ますが、果たして和算ではどう計算するのか? 答えを出せるということは、サイクロイド界隈の知識はあったということでしょうね。
和算のサイトの記述に揃えて円の直径を \(D\) とします。すると半径の値は \(D/2\) なので、以上により、サイクロイド部分の軌跡の長さはこれを使って
$$8r = 8 \times D/2 = 4D$$

その２：円が菱形の角をぐるっと回る部分での点の移動距離
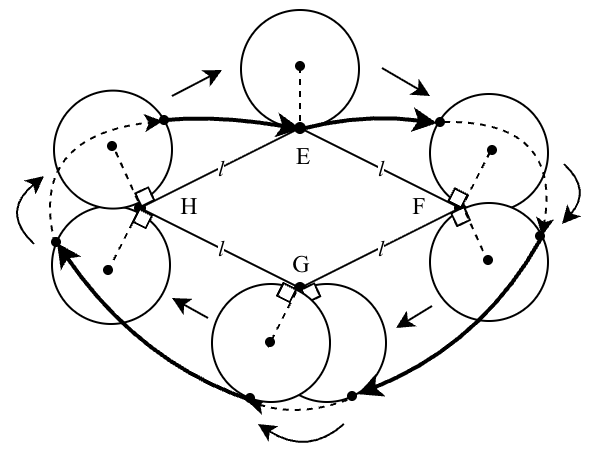
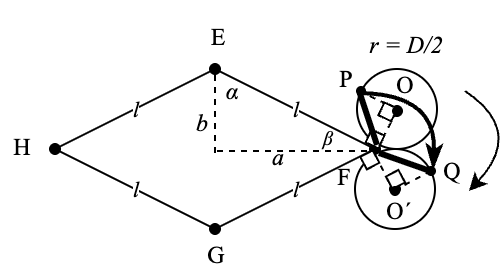
計算で使う変数と辺や角の説明のために以下の図にしたがって説明と計算を続けます。（作図が悪いですねー。でもとりあえずこれでお願いします）

角をぐるっと回るのは、菱形の角F、G、Hの三箇所で起こります。以下、それらを順に計算します。
円が角でぐるっと回るとき、円上の点は、PからQへFを中心とした扇形の弧を描きます。この長さを計算します。

菱形の角Fでの扇形の軌跡について、

• 扇形の半径： 円（上側）の図で、上の「円の自転もトータルで1回転である」という条件から、円が菱形の角Fに着いたとき、円は90度分自転していることになり、よって角PFOは45度。すると三角形FOPは45度を二つ持つ二等辺三角形で、円の半径は \(D/2\) であることからピタゴラスの定理を使って
  $$ \mathrm{PF} = \sqrt{(D/2)^2 + (D/2)^2} = {\sqrt{2} \over 2}D $$
• 扇形の中心角：FOと水平がなす角は \(\alpha\) に等しい。したがって扇形の中心角は \(2\alpha\) 。ここで菱形の \(1/4\) の形の直角三角形に三角関数を当てはめると、そのアークサインの式より
  $$ \alpha = \sin^{-1}{a \over \sqrt{a^2 + b^2}}$$
• 扇形の弧の長さ：以上2つの値より弧の長さは、半径×中心角（ラジアン）で、
  $$ \mathrm{PF} \times 2 \times \alpha = {\sqrt{2}}D \times \sin^{-1}{a \over \sqrt{a^2 + b^2}}$$

以下、他の角でも同様に計算します。

菱形の角Gでの扇形の軌跡について、
以下の図のような円の動きになります：

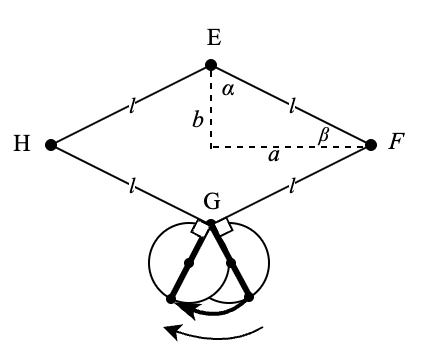
角Fの場合とよく似ていますが、円は角Gに到達した時点で1/2回転（180度）分自転しているので、黒点も1/2回転した（180度の）位置にあります。すると今度の扇形の半径は円の直径に一致し、値は \(D\) になります。円が角Gの周りをぐるんと回る角度は図形的考察で \(2\beta\) です。
\(\beta\) の値は \(\alpha\) と同じようにアークサインを計算することにより
$$ \beta = \sin^{-1}{b \over \sqrt{a^2 + b^2}}$$
よって黒点が描く扇形の弧の長さ（半径）×（中心角（ラジアン））はそれぞれ値を代入することにより
$$D \times 2 \times \beta = 2D \sin^{-1}{b \over \sqrt{a^2 + b^2}}$$

菱形の角Hでの軌跡について、
角Fでの円の向き変えと全く同じ動きが角Hでも発生して、同じだけの軌跡を描く（細かく言うと、角Fでは点が円上の90度の位置にありましたが、角Hでは270度の位置にあるので、描く扇形の半径は対照な位置で長さも同じ、みたいな。図を描くべきか）。よって値も同じで

$$ \mathrm{PF} \times 2 \times \alpha = {\sqrt{2}}D \times \sin^{-1}{a \over \sqrt{a^2 + b^2}}$$

菱形の角Eでの軌跡について、
円が角Eにいるときは円上の点がちょうど菱形の角の位置にあるので、円がぐるんと動いても扇形が発生しない。したがって軌跡の長さへの貢献はゼロ。

最終的な答え

というわけで問題で出てくる軌跡の各部分の長さの計算が完了しました。これらを全てまとめたのがトータルの軌跡の長さになります。

（菱形4辺分のサイクロイドの軌跡）＋（角Fでの扇形の弧の軌跡）＋（角Gでの扇形の弧の軌跡）＋（角Hでの扇形の弧の軌跡）

すなわち
$$
\begin{align}
&4D + \sqrt{2} D \sin^{-1}{a \over \sqrt{a^2 + b^2}} + 2D \sin^{-1}{b \over \sqrt{a^2 + b^2}} + \sqrt{2} D \sin^{-1}{a \over \sqrt{a^2 + b^2}} \\
&= 4D + 2D \left(\sqrt{2} \sin^{-1}{a \over \sqrt{a^2 + b^2}} + \sin^{-1}{b \over \sqrt{a^2 + b^2}} \right)
\end{align}
$$

とりあえず

解答らしきものに辿り着きましたが、和算のサイトにある答えと一致しました、よかった。が、これが上で引用した和算の漢字だらけの解と一致するらしい… うーん数学よりそっちの解読の方がはるかに難しいです。しかし、AI翻訳をかけた文章を読むと、確かに同じことを計算しているような感じがします（翻訳後もまだ完全には意味が取れていない）。

少し補足
上記の答えには \(a\) 、\(b\) 、\(D\) という変数があり、それは算額のサイトの解説に従ったものですが、「円が菱形の周りを一周したとき、円自体もちょうど一回転する」という条件（注：元の漢文の問題が完全解読できた時に検証します）があるようで、その条件があるならば、「円の周長＝菱形の周長」が成り立ち、それを式で書くと \( 2 \pi \cdot D/2 = 4 \sqrt{a^2 + b^2} \) ですね。というわけで \(a\) 、\(b\) 、\(D\) のうち独立な変数は2つになります。

と、この最初の問題だけでもフォローすべき箇所がいくつかありますが、今のところこの辺で。

ここまでのまとめ

今のところ算額から得られた知識をまとめるとすれば

• 牟礼神社には算額があり、その年代は明治31(1898)年、と算額としては比較的新しい
• 算額の第一問目はサイクロイドの一種を問題にしている。そこから以下のことが推測される：
  • サイクロイドおよびそれに類似した曲線を対象にする数学が当時あった
  • その数学を解析するために必要な積分や三角関数等、少なくともそれらの機能に相当する⁷知識もあった
  • 必要な数学は基本的な図形問題の知識と三角関数なので、今なら高校生でも何とか解ける?

という感じかな、と思います。

サイクロイドの数学とか、和算では円の性質とかを純粋に数学的に追究して生まれたのでしょうか。あるいは西洋、あるいは中国（中国語でサイクロイドに相当する擺線という単語があるので）の数学が入ってきていたのでしょうか。
時代的には、明治31年といえばすでに鉄道が開通していて牟礼駅（明治21年〜）もありました（鉄道の開通が思ったより早い）。実は、蒸気機関車の駆動輪上で駆動の棒が接続されている部分を機関車が走っているときに横から眺めたらその軌跡はサイクロイドだったりします。多分この問題とは関係ないでしょうが。

個人的な感想

今回は何だか昔の人と数学を共有できた気がします。江戸や明治の人が書いたものとかを見る機会、さらにはその内容を確かめるなんてそうそうないじゃないですか? そして書かれたのが飯綱町の昔の方で。そしてそれが数学で。
結果として数学としての内容はほぼ理解しましたし、自分でも計算できることを確かめました。なるほど、算額というのはこういう問題を扱うものなのだなあと（ってまだ一題調べただけですが）。

それにしても江戸や明治時代の数学が今こうやってたどることができるなんて、不思議な気分であり、問題の全体が分かった時はちょっと感動みたいなものがありました。ドクターストーン（漫画・アニメ）⁸の主人公じゃないですが、

唆る（そそる）ぜこれは…!

ドラマや漫画での架空の話⁹が現実に自分の身に起こったような感覚、と言ったら大袈裟でしょうか。

ただし、今回やったのは「算額の問題を現代の数学で解く」であって、数学の問題としては理解しましたが肝心の「和算」の実際には全然触れられていません。「和算ではこんな問題を扱うんだな」、と言うのは少しわかった感じですが、実際にどう解いていたのかというのが。
実際に和算ではどう解くのか、いつかちゃんと調べてみたいと思います。

脚注：

1. 明治31年ともなれば既に西洋風の教育がなされていたのではないかと… それでも和算を続けていたのかなという素朴な疑問が → どうやらこの時代ぐらいから学校で西洋数学を教えるようになったようです。和算のほぼ最終の時代だったようです。 ↩︎
2. 他の算額の本によると、どうやら同じ問題が同じ方によってこれより以前に別の神社に奉納されているようで、問題自体はもっと古いようです。 ↩︎
3. 「和算の館」にある解説に現代語での問題の概略はありますが、数学の問題として挑むためには結局問題の原文を詳細に読解する必要があるので。 ↩︎
4. もしかすると楕円とサイクロイドを混同している可能性もある? ただその場合でも計算結果は合ったりもするような。よくわかりません。 ↩︎
5. この条件がないと、円が菱形の角に来たときに黒点が中途半端な角度の位置になり、計算が面倒になりますね。 ↩︎
6. そうだとすると、ここで描いた図では円が小さすぎますね。円が菱形の周りを転がる間にちょうど1回転の自転があるならば、菱形の1辺＝円の1/4の周長でないといけないので。 ↩︎
7. 例えば円の面積を計算するとき、積分法を知っていれば円の曲線の式を積分すればいいですが、一方で積分を使わずとも、円周は半径の \(2\pi\) 倍（\(l = 2 \pi r\)）である、ということさえ知っていれば、円の面積は円を細い三角形に分割・並べ替えすることで公式 \(S = \pi r^2\) にたどり着ける（←まあこれ自体が積分みたいなものですが）、というのは確か中学校で習いましたっけ? そういう感じで、積分計算はなくても特定の図形の面積の計算はできたのかなと。 ↩︎
8. SF的設定で、現在の少年少女が未来の、文明が滅亡した地球で目覚め、そこからかつての科学技術を自らの手で取り戻していくというストーリー。 ↩︎
9. 他には、「JIN-仁-」という、医者が江戸期にタイムスリップするという漫画・ドラマがありましたが、もしその数学版というものがあれば… なんて。 ↩︎