今までに二題目まで解説してみましたが
一題目、二題目、と徐々に難易度が上がっているというか、問題が複雑になってきているような気がします。何はともあれ、牟礼神社の算額にある三つの問題のうち二つまで一応解説したので、最後の問題も、算額の本の説明をもとに解法を解説したいと思います。
今回もやることは同じです。まずは算額にある問題を数学として理解する、それにはまず解いてみる、ということで、今の数学の方法での解き方、の解説をしてみたいと思います。
問題の引用
以下は電子書籍「算額への招待」からの引用です:
細かい話に入る前に
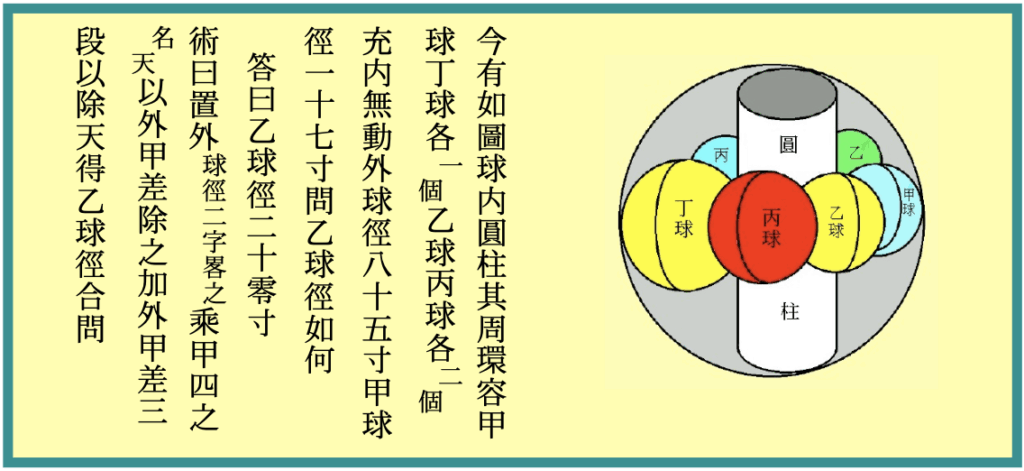
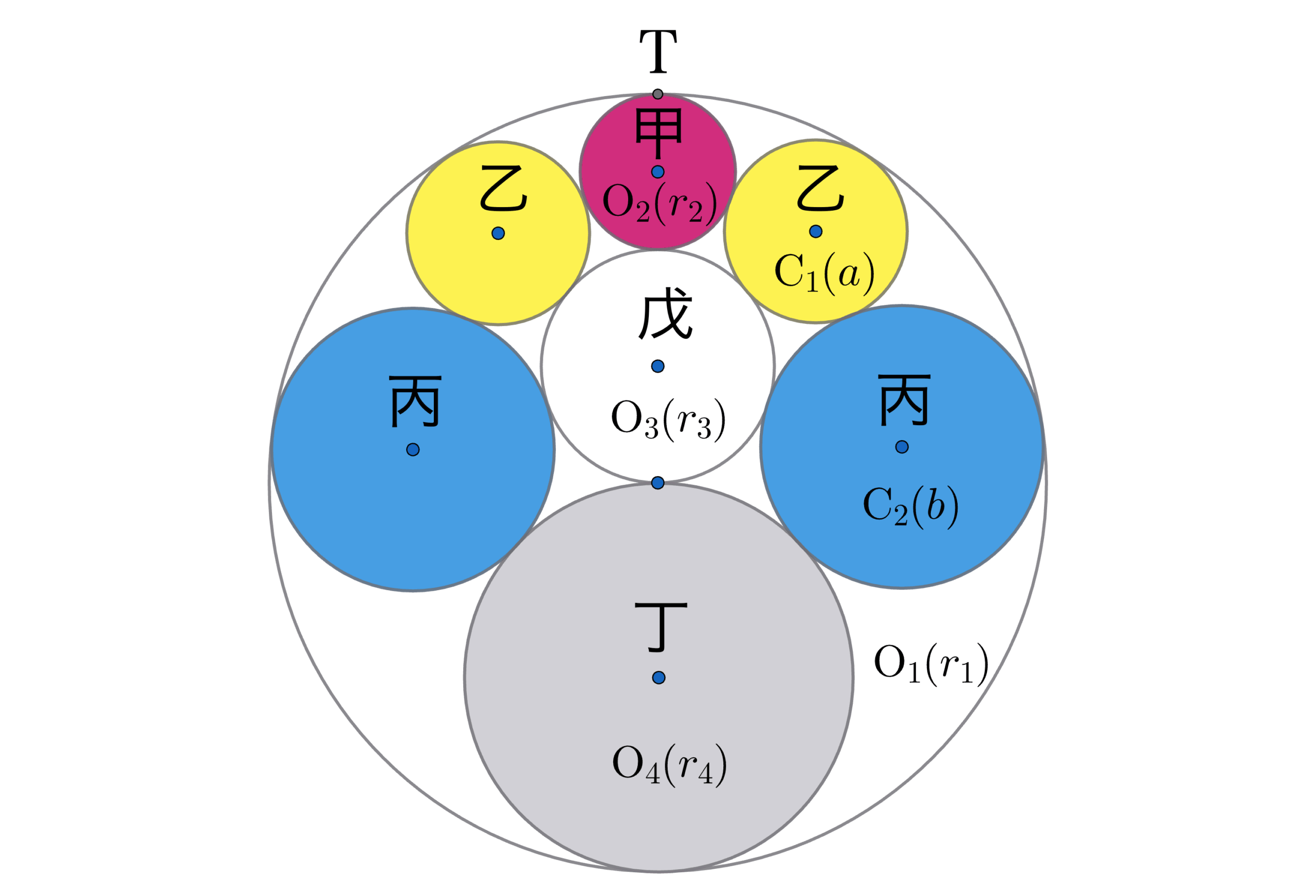
この問題をざっくり説明すると「図のような配置で球をうまく詰められたとして、それぞれ大きさはどうなるか計算しなさい」という感じです。
で、色々な数式を使ってああだこうだやるのが以下の話なんですが… あまりそこら辺には興味がない場合でも、このページの冒頭の図を少しだけ眺めてみてもらえますでしょうか。これは問題にある図の、真ん中での水平断面図です。
実はこの断面図はある意味解答になってます。この問題に出てくる全ての球の大きさを計算して、正しいサイズ比でそれぞれの球を描いてあるからです。
どうでしょう… なんというか、見事なサイズで球が収まっていると思いませんか? 正しいサイズ比だから、全ての球がきちんと収まっているとも言えます。
そういうものを数学で導き出す、というのがこの問題だと思っていただければいいかと思います。
問題文と回答文の文字起こし
まずは引用した算額の問題文の画像より文字起こしをしてみます。
問題文:
それは以下のとおりです(上の算額の画像から文字データを抜き出しました)
今有如圖球内圓柱其周環容甲球丁球各(一個)乙球丙球各(二個)充内無動外球徑八十五寸甲球徑一十七寸問乙球徑如何
DeepL翻訳:
図のように球の内側に円柱があり、その周縁には甲球と丁球が各一つ、乙球と丙球が各二つ収まる。内部は空洞で、外側の球の直径は85寸、甲球の直径は17寸である。乙球の直径はいくらか。
そして解答文:問題文同様、算額の画像からの文字データの抜き出しです
答曰乙球徑二十零寸術曰置外球徑二字畧之乘甲四之名 天以外甲差除之加外甲差三段以除天得乙球徑合問
DeepL翻訳:
答曰:乙球の直径は二十寸である。術曰く:外球の直径二字を略し、甲四を乗じる。天の外甲差を除き、外甲差を加える。三段に分けて天を除き、乙球の直径を得る。問に合する。
問題の概観
複数の球を決められた図形の中に収めたときの問題、これ自体は和算の問題としてよく見かけますが、この問題の場合、球の数が多いことが気になります。そして、どうやら一つの球の大きさが他の球にもしっかり影響を与えるように見え、「実はどれかの球だけ単独で計算できて複雑さが下がる」ようなものではなさそうです。
その結果、少なくとも計算がかなり複雑になり、問題が持っている条件を十分に見出せずに解を求めらない、ということもありそうです。
問題の二次元図
今回の問題は、問題に出てくる球が水平面上に並ぶので、それらの球の中心を通る水平な断面で考えることにより、二次元で複数の円が接する問題になります。さらに、球の配置が左右対称なので上から見て真ん中より右側だけの球で計算すればいいです。
といったわけで断面図が以下のようになり、真ん中より右側の球にだけ今の数学っぽい名前を振ります:
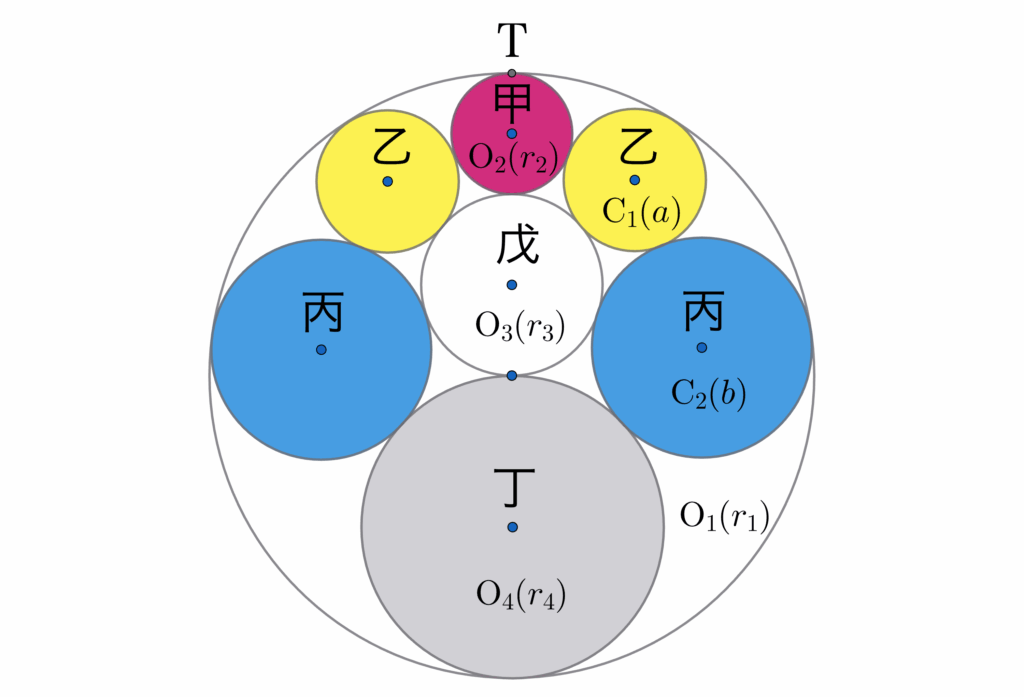
上の図では半径 \(r\) を持つ、外円と接している円のことを \( \mathrm{C}(r) \) と書いています。同様に真ん中に縦に並ぶ円を \( \mathrm{O}(r) \) と書くことにします。
今回使う数学:反転幾何学
ところで、今回の問題の一つの特徴は、
「問題に沢山の円が出てくる、そして円しか出てこない」
ことです。よくあるパターンの「円が直線に接している」とか「三角形に円が内接している」とかではなく「円の中に複数の円が接している」ですね。このような幾何の問題に使えそうな定理や公式等はあまり一般的ではない感じがします。すなわち解法の苦戦が予想されます。
そこで:幾何学の世界には円を別の円ないし直線に変換して考える手法がありまして、それは「反転幾何学」(Inversive Geometry) というものです。その「反転」を使えば、例えば「円と円の問題」を「円と直線の問題」として扱うことができます。円と直線に関する定理(関係式)は、色々ありますので、後者の方が扱いやすいです。
数学の世界には「元の問題を直接解かずに、何かの変換をかけて問題を解きやすくしてから解く」タイプのアプローチが多々あります。簡単なものでは例えば円を二次元の座標上で扱うとき、普通に \( (x, y) \) の座標(直交座標)でなく \( (r, \theta) \) (半径と角度、極座標)で表すとか… もっと本格的なものではある種の方程式をフーリエ変換やラプラス変換で解くとかですか。どのような変換が適切かは、その時々の問題の性質に応じて決められます。今回使う「反転」もそのようなもの(問題へのアプローチ)です。
反転の定義のおさらい
先に進む前に「反転」に関して軽く説明します(「軽くない」説明は、適宜数学の本やネット上の情報で補っていただけますでしょうか)。
平面上の点 \(\rm{P}\) に対して、反転の原点 \(\rm{O}\) と反率 \(k\) を定め、以下の図のように \( \overline{\rm{OP}} \cdot \overline{\rm{OP’}} = k\) となるような点 \(\rm{P}’\) を定める変換を反転といいます。
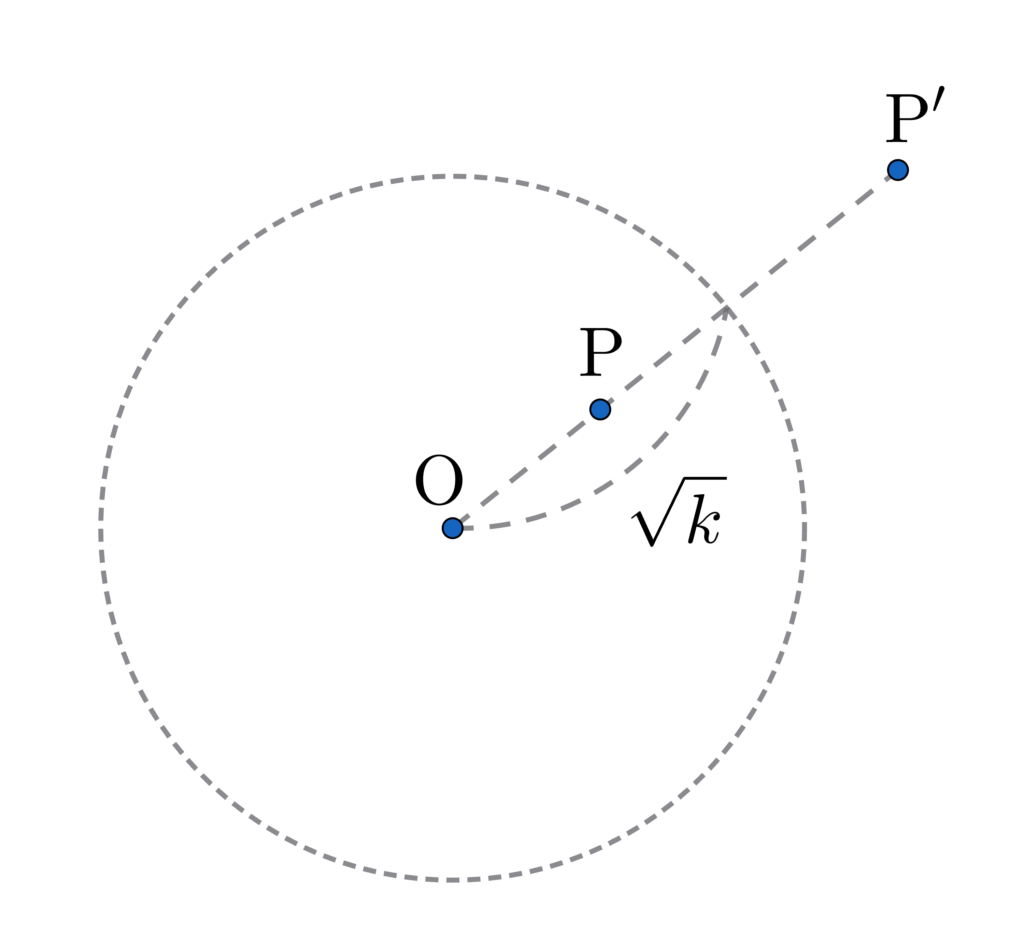
反転には
- 直線は直線または円に変換される
- 円は円はまたは直線に変換される
といった性質があり(「または」の部分は細かな条件でどちらかが選ばれる)、この性質をうまく使って幾何の問題に適用すれば、問題の図形が簡略化でき、今回のような複雑そうな問題にも威力を発揮する… はずです。
この問題で用いる反転の性質
この問題には、上で出した図の通り円しか出てきませんので、円と反転の関係に注目する必要があります。後で詳細を説明しますが、今回の問題の場合、反転の原点を適切に選ぶことにより、以下の2つの種類の変換を考えることになります:
- 反転の原点を通る円 → 直線に変換
- 反転の原点を通らない円 → 半径と中心が異なる円に変換
そこでこの二つの種類の変換が満たす性質を以下に紹介します。
反転の原点を通る円の反転
- 反転の原点を通る円は、反転により直線に変換される。
- 反転される前の円の半径が \(r\)、反転の反率が \(k\) のとき、反転後に移った直線と反転の原点との距離 \(d\) に関して $$
d = {k \over 2r} \tag{1}\label{inv-line-distance} $$ になる。
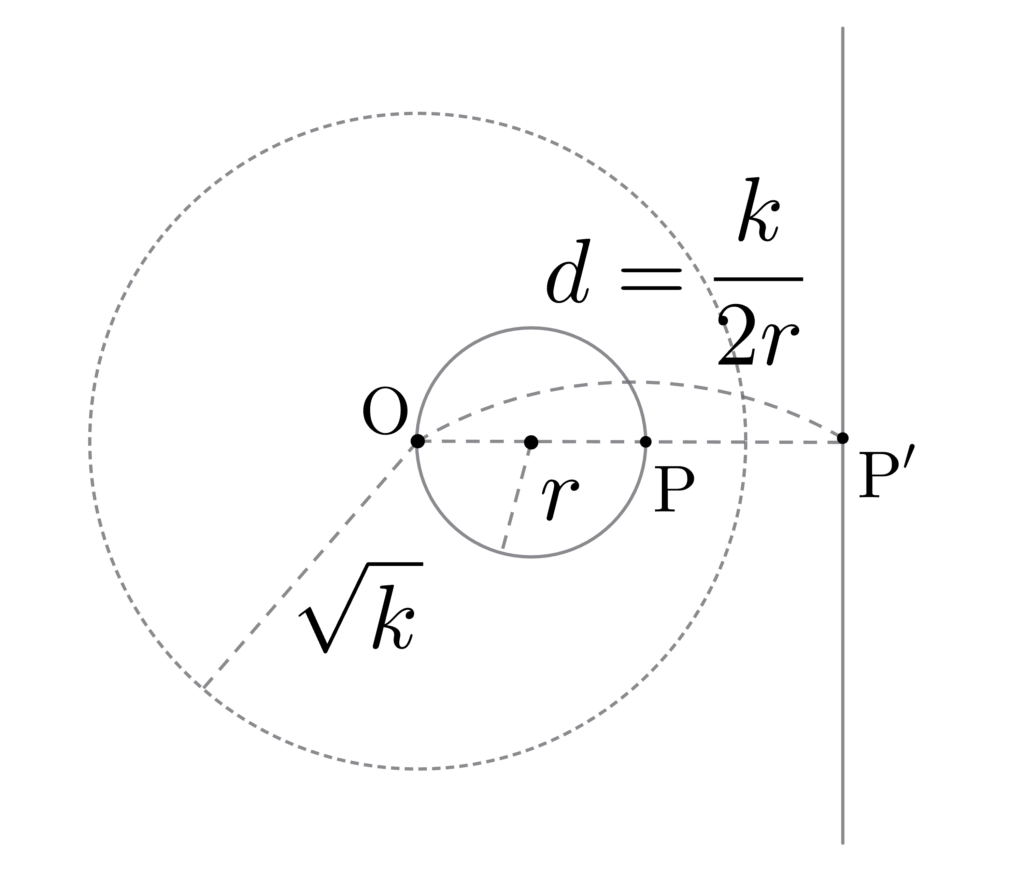
簡単な証明: \(\overline{\rm{OP}} \cdot \overline{\rm{OP’}} = k\) で、\(\overline{\rm{OP}} = 2r\) より \(\overline{\rm{OP’}} = k / 2r\) 。\(\overline{\rm{OP’}} = d\) でなのですなわち \(d = k / 2r\)。
反転の原点を通らない円の反転
- 反転の原点を通らない円は、元の円とは中心と半径が異なる円に変換される。
- 反転の原点から反転前の円に対して接線を引くと、その接線は反転後の円の接線でもある。なぜならその接線は反転の原点を通るから反転後には同じ直線に移され、一方反転の性質により直線と円と接点の関係は保存されるからである。
ここで原点が \(\rm{O}\) の反転の反率を \(k\) 、反転前の円の半径を \(r\) 、反転後の円の半径を \(r’\)、接線が反転後の円と接する点を \(\rm{P}’\) とすると次の関係が成り立つ:$$
{r’ \over r} = {\overline{\rm{O}\rm{P}’}^2 \over k} \tag{2}\label{inv-rad-ratio}
$$
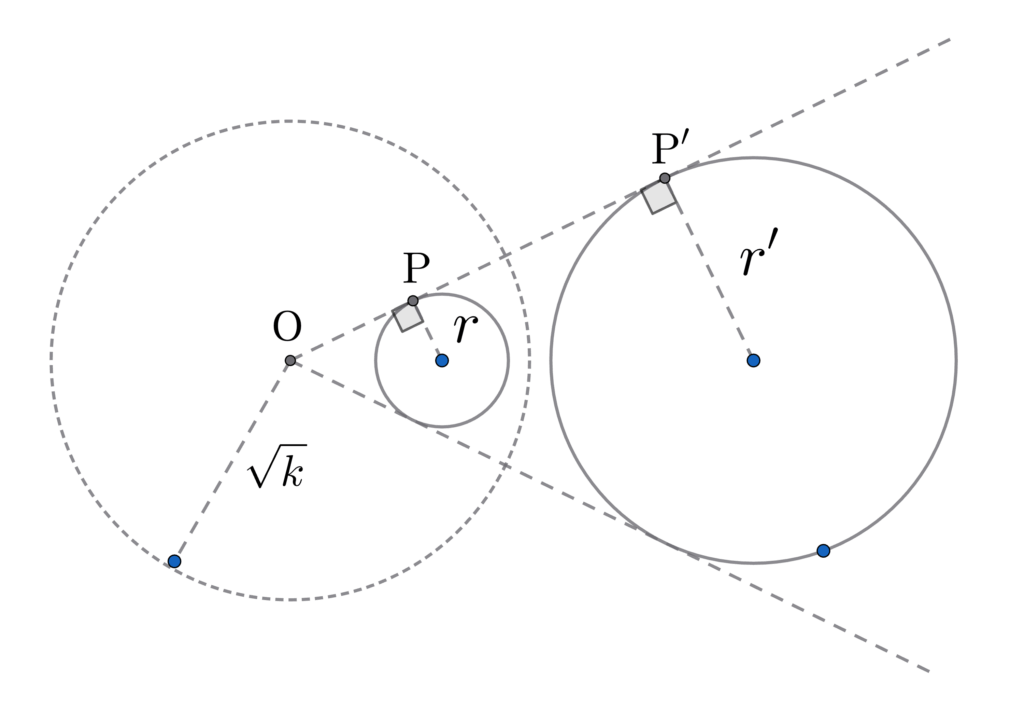
簡単な証明:\(r’/r = \overline{\rm{OP’}} / \overline{\rm{OP}}\) で、 \(\overline{\rm{OP}} \cdot \overline{\rm{OP’}} = k\) より \(\overline{\rm{OP}} = k / \overline{\rm{OP’}}\)、よって \(\overline{\rm{OP’}} / \overline{\rm{OP}} = \overline{\rm{OP’}} / (k / \overline{\rm{OP’}}) = \overline{\rm{OP’}}^2 / k\)、すなわち \(r’ / r = \overline{\rm{OP’}}^2 /k\)。
この問題における反転の適用
この問題の条件、および円の配置を再確認してみますと、構成要素のうち、外円と甲は
- 半径が与えられている
- 上の図において点 \(\rm{T}\) で接している
以上のことから、点 \(\rm{T}\) を反転の原点として反転をすれば
- 外円と甲は反転の原点 \(\rm{T}\) を通る円なので、それぞれ直線に移される=円が二つ減り、それぞれ直線に変換される。
- 外円と甲以外の円は円に移され、外円と甲が反転されてできた2つ直線の間に収まる。
- 元々接していた円同士は、反転の後も接している(外球あるいは甲に接していた円はそれらの反転後の直線と接する)。
という、幾何の問題としてより好ましい状況になります。具体的には、反転を施した後は以下のような配置になります:
元の断面図は

でしたがこれが反転後は:
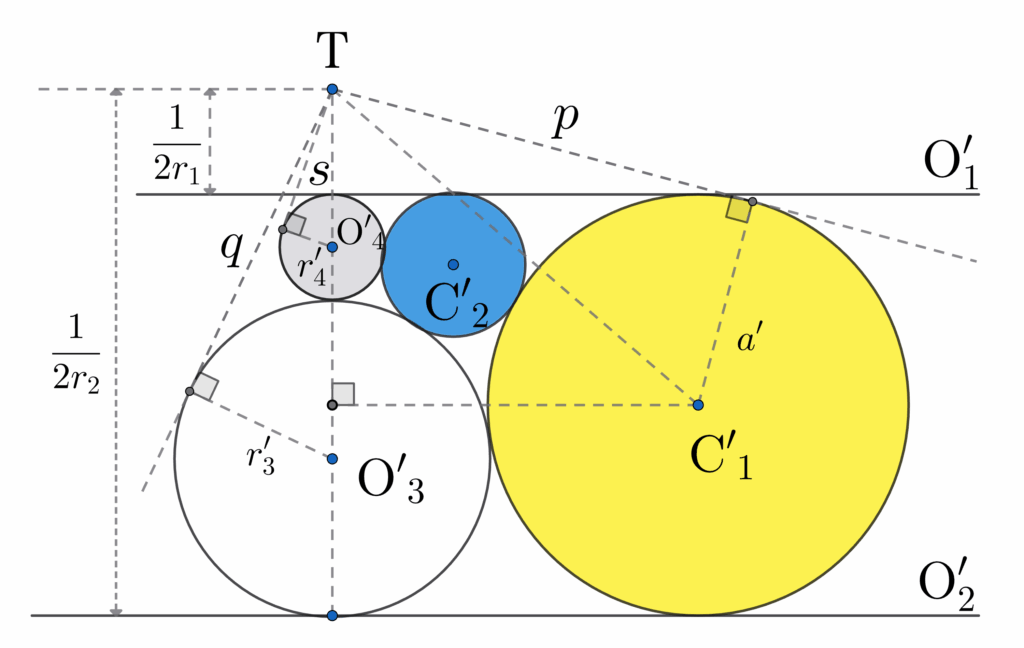
外周円の円周は水平な直線の \(\mathrm{O}_1′ \) に、 マゼンタ(赤紫)の甲の円周は\(\mathrm{O}_2′ \) に移され、元々それらの間の空間に埋め込まれていた乙、丙、丁、戊の円は反転後も移った後の甲と外周の間に埋め込まれている感じです。
二つの図を比べるに、円の大小関係と上下の位置関係が逆になっています。これが「反転」と呼ばれる所以なのだと思います。
ぱっと見で、元の、円の中に円が複数詰め込まれた図より、反転後の、円と直線の組み合わせの図の方が扱いやすそうですよね? 例えばこの図から「大きさが異なる二つの円に共通の接線が接している」問題を解いたりしていけばよさそうですが、それは割と見かける問題ですね。これが反転を施してから問題を解くことの利点です。
先に進む前に:円と接線の補助定理
反転を使うことで、円同士が接する問題が円と接線の問題になりました。というわけでこれから問題を解くのに必要な「道具」は円と接線に関する関係式です。そういったものをいくつかさらっておきます。証明は省略します。
その1
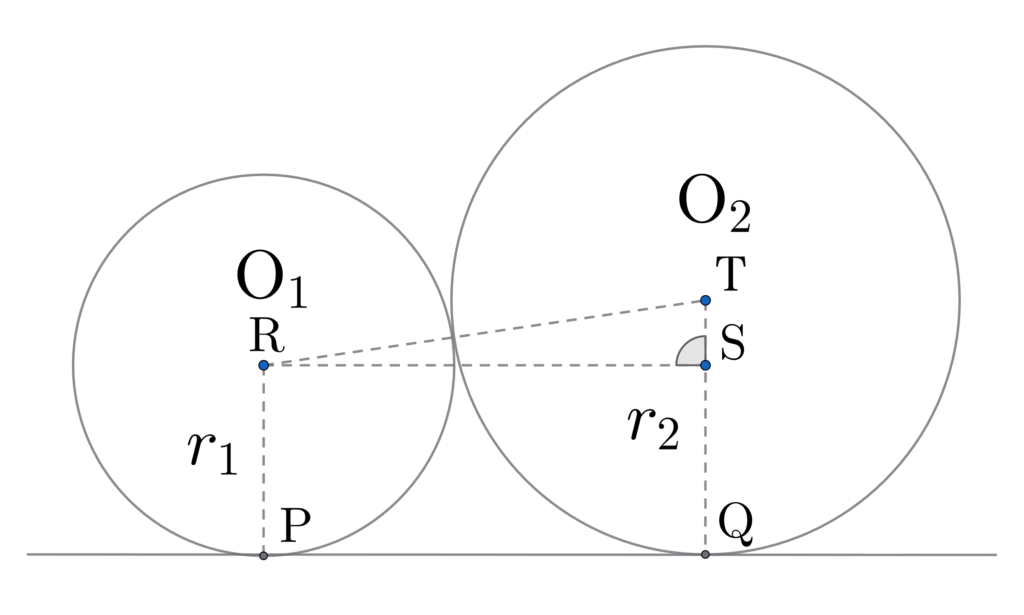
二つの大きさが異なる円が共通の接線に接している時、接線上の接点間の距離(図の \( \overline{\rm{PQ}}\))は
$$
\overline{\rm{PQ}} = 2 \sqrt{r_1 r_2} \tag{3}\label{two-circle-dist}
$$ になる。
その2
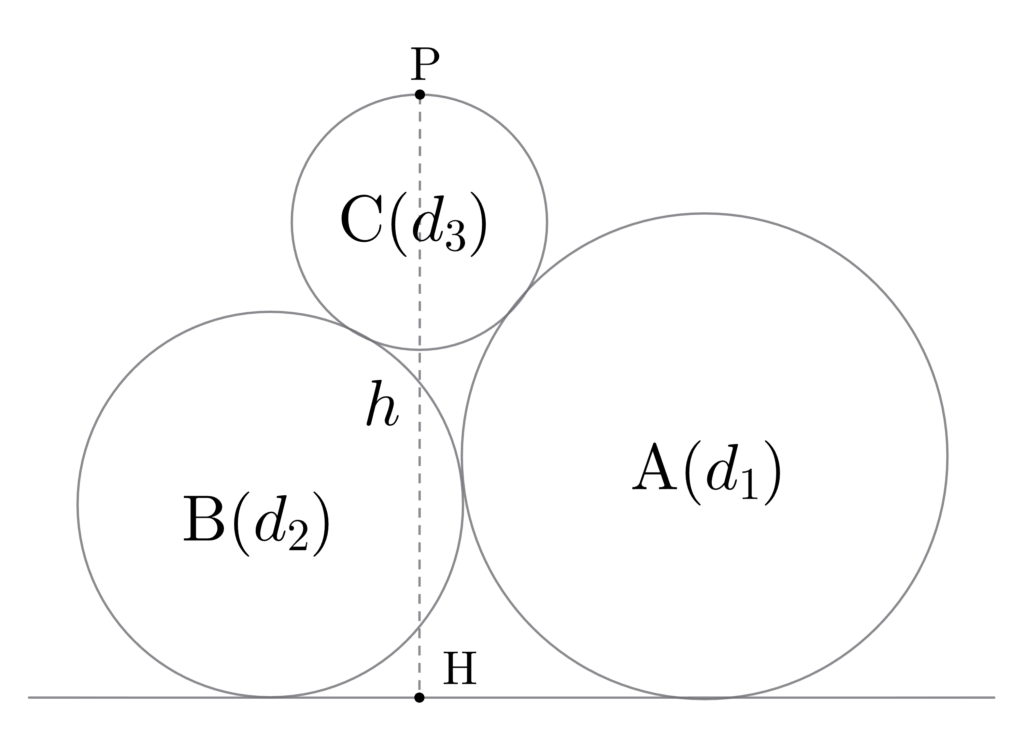
以下の図のような関係にある3つの円と接線に関し(\(d_1\)、\(d_2\)、\(d_3\) は円の直径、\(\overline{\rm{PH}} = h\) とする)、以下の式が成り立つ:$$
d_3 = {\left\{(d_1 + d_2)h \,-\, d_1d_2\right\}^2 \over 4d_1d_2 h} \tag{4}\label{three-circle-lemma}
$$
それでは解法の開始
前置きが長くなりました。今回の問題はそれなりのお膳立てが必要ということでもあります。ここから問題の解法に入ります。
まず反転の適用(上で既にその図を示しましたが)ですが、反転の原点を外の円と甲の円の接する点に、反率は \(1\) として反転を問題の図に適用します。
次にこの反転後の図における関係式を列挙し、その後に方程式を解いていきます。問題に出てくるそれぞれの円の半径が変数で、それらの連立方程式になります。円がたくさんあるので大変ではあります。元の問題で求めているのは乙の半径、すなわち \(a\) の値1でしたね。
あと、問題で与えられた条件、外円と甲の半径はそれぞれ \(r_1\) と \(r_2\) で、すなわち \(r_1\) と \(r_2\) は定数であることに注意します。
反転における円とその接線の関係 \eqref{inv-rad-ratio}(\(k = 1\) の場合)を \(\mathrm{C}_1’\) に適用すると$$
{a’ \over a} = {p^2 \over 1} = p^2
$$ ここで \(p^2\) の値は反転図上で直角三角形を見出してピタゴラスの定理を使うことにより $$
\begin{aligned}
p^2 & = \left( {1 \over 2r_1} + a’ \right)^2 + \left( \sqrt{a’r_3′} \right)^2 \,-\, a’^2 \\
& = {1 \over 4{r_1}^2} + {a’ \over r_1} + 4a’r_3′
\end{aligned} $$ したがって $$
{a’ \over a} = {1 \over 4{r_1}^2} + {a’ \over r_1} + 4a’r_3′ \tag{5}\label{p-eqn}
$$ 同様に円 \(\mathrm{O}_3’\) の半径と接線の長さに注目して $$
{r_3′ \over r_3} = {1 \over {4 r_2}^2} \,-\, {r_3′ \over r_2} \tag{6}\label{r-eqn}
$$ および円 \(\mathrm{O}_4’\) の半径と接線の長さに関して $$
{r_4′ \over r_4} = {1 \over {4r_1}^2} + {r_4′ \over r_1} \tag{7}\label{s-eqn}
$$ 2つの円と共通接線上の接点間の距離\eqref{two-circle-dist}に関して、(\(\mathrm{O}_4’\) と \(\mathrm{C}_2’\) の接点間の距離)+ (\(\mathrm{C}_2’\) と \(\mathrm{C}_1’\) の接点間の距離)=(\(\mathrm{O}_3’\) と \(\mathrm{C}_1’\) の接点間の距離)であるから $$
2\sqrt{b’r_4′} + 2\sqrt{a’b’} = 2\sqrt{a’r_3′} $$ 整理すると $$
\sqrt{b’r_4′} + \sqrt{a’b’} = \sqrt{a’r_3′} \tag{8}\label{two-circle-dist-2}
$$ また、2つの平行直線 \( \mathrm{O}_1’\)、\(\mathrm{O}_2’\) 間の距離とそれらの間で両者に接している円 \(\mathrm{C}_1’\) の直径は等しいので $$
{1 \over 2r_2} \,-\, {1 \over 2r_1} = 2a’$$ これを \(a’\) に関して整理すると $$
a’ = {r_1 \,-\, r_2 \over 4r_1r_2} \tag{9}\label{a-dash}
$$ \(a’\) を \(r_1\) と \(r_2\) で表すことができました。いいですね。一番最初に出てきた \(a\) の式\eqref{p-eqn}で、あとは \(r_3’\) が消えればいいのですが… もっと計算が必要なようです。
2つの平行直線 \( \rm{O}_1’\)、\(\rm{O}_2’\) 間に挟まれて並ぶ円で、(\(\mathrm{O}_3’\) の直径)+(\(\mathrm{O}_4’\) の直径)=(\(\mathrm{C}_1’\) の直径)になっているので$$
2r_3′ + 2r_4′ = 2a’ $$ これを整理して $$
r_3′ + r_4′ = a’ \tag{10}\label{r3-r4-a-dash}
$$ 反転前の図で、外円の直径と縦に並んだ3つの円の直径の関係から$$
r_2 + r_3 + r_4 = r_1 \tag{11}\label{ext-circle-and-int-three-circles}
$$ もう一つ関係式が使えます。3つの円と一つの接線がある場合に成り立つ式\eqref{three-circle-lemma}を反転後の3つの円 \(\mathrm{O}_3’\)、\(\mathrm{C}_2’\)、\(\mathrm{C}_1’\) に適用すると$$
2b’ = {\left\{\left( 2a’ + 2r_3′ \right) \cdot 2a’ \,-\, 2a’ \cdot 2r_3′ \right\}^2
\over
4 \cdot 2a’ \cdot 2r_3′ \cdot 2a’}
$$ これを整理すると $$
b’ = {{a’}^2 \over 4r_3′} \tag{12}\label{b-dash}
$$
ここまでで反転図から必要な関係式を抜き出したので、あとはそれらを使って変数を消去していって \(a\) を \(r_1\) と \(r_2\) だけで表すのが目標です。既に \eqref{a-dash} 式で \(a’\) は \(r_1\) と \(r_2\) だけで表せているので、以降の式では \(a’\) もいわば定数としてみなしていいです。
\eqref{r3-r4-a-dash} 式は実質 \(r_3’\) と \(r_4’\) の式なので、もう一つ \(r_3’\) と \(r_4’\) に関する式が作れれば \(r_3’\) と \(r_4’\) が計算できます。
それには、\eqref{two-circle-dist-2} がほぼ \(r_3’\) と \(r_4’\) なのですが \(b’\) がまだ未知、そこで\eqref{b-dash}を代入して計算することにより$$
r_3′ = {a’ \over 2} + {\sqrt{a’ r_4′} \over 2} \tag{13}\label{r3-dash-dash}
$$ これで \(r_3’\) と \(r_4’\) の式になりましたので \eqref{r3-r4-a-dash} と \eqref{r3-dash-dash} を組み合わせます。\eqref{r3-dash-dash} 式を変形すると$$
\left(r_3′ \,-\, {a’ \over 2} \right)^2 = {a’ \over 4} r_4′
$$ ここに \eqref{r3-r4-a-dash} 式より \(r_4’\) を代入して$$
\left(r_3′ \,-\, {a’ \over 2} \right)^2 = {a’ \over 4} \left( a’ \,-\, r_3′ \right)
$$ 展開してまとめると$$
{r_3′}^2 – {3 \over 4}a’r_3′ = 0, \space r_3’\left(r_3′ \,-\, {3 \over 4}a’\right) = 0
$$ \(r_3′ \ne 0\) より$$
r_3′ = {3 \over 4}a’ \tag{14}\label{r3-dash-answer}
$$ \eqref{p-eqn} に \eqref{a-dash} および \eqref{r3-dash-answer} を代入して$$
{a’ \over a} = {1 \over 4{r_1}^2} + {a’ \over r_1} + 4’a \cdot {3 \over 4}a’
$$ 上で書きましたが \(a’\)は既に \eqref{a-dash} 式で \(r_1\) と \(r_2\) で表されているので既知、したがって \(a\) に関してはこれ以上方程式を解く必要はありません。上の式より$$
\begin{aligned}
{a’ \over a} &= {1 \over 4{r_1}^2} + {a’ \over r_1} + 4’a \cdot {3 \over 4}a’ \\
&= {1 + 4a’r_1 + 12{r_1}^2{a’}^2 \over 4{r_1}^2}
\end{aligned}$$ この式の分母分子を反転させ、整理すると$$
a = a’ \cdot {4{r_1}^2 \over 1 + 4a’r_1 + 12{r_1}^2{a’}^2}
$$ この式に \(a’\) の式 \eqref{a-dash} を代入し、整理することで以下の式を得ます:$$
a = {4r_1r_2(r_1 \,-\, r_2) \over 3{r_1}^2 \,-\, 2r_1r_2 + 3{r_2}^2}
$$ この答えは算額の解説の答えと合っています。よかった。ちなみに算額の解答文に形が合うようにこれを変形すると$$
a = {4r_1r_2 \over {\displaystyle 4r_1r_2 \over \displaystyle r_1 \,-\, r_2} + 3(r_1 \,-\, r_2)}
$$ となります(天 = \(4r_1r_2\) 、外 = \(r_1\) 、甲 = \(r_2\) 、乙 = \(a\) に相当)。
しかし和算では変数は漢字なんですか。ここまで和算の算額の問題のことを書いてみたものの、まだ実際の和算というものに踏み込んでいないのですが(純粋に数学の問題としてのみ扱った)、漢字の変数で数式を扱うとか、個人的にはちょっと想像できません。面倒過ぎないですか? せめてカタカナの方が楽な気も。中国から伝わった算術の伝統を維持してたのですかね(大昔の数学が西洋から中国に伝わったとき、色々漢字化されて、それが日本に伝わったようです)。
とりあえずのまとめ
牟礼神社の算額にあった三題の問題のうち、これが一番難しいのではないでしょうか。難しいし、いろんな関係式を使うので解法の計算量も多くなりました。
今回説明した解法は反転幾何学がベースになっていますが、個人的に不慣れで最初は戸惑いました。高校の数学のカリキュラムでは反転幾何学を正式には習っていないと思います。でも、受験の問題や、数学のコンテストみたいなものでは出題されるようですね。
脚注
- ここでは元の問題設定に従い \(a\)、すなわち甲球の半径を求めるのがメインですが、他の球の半径も求められます。それらの値も自明ではないので別途計算を解説してみようかと思います。ちなみにこの記事に載せた問題の断面図(反転前)は適当に甲〜戊の円を描いたわけではなく、どの円も計算に基づいた半径(の大きさの比)にしてあります。 ↩︎
コメント